We got this issue couple of days back where we needed to smooth a line graph like below. It seemed strange that this was not as trivial by the Bezier methods provided by Core Graphics. So we embarked on a journey to find a generic solution.

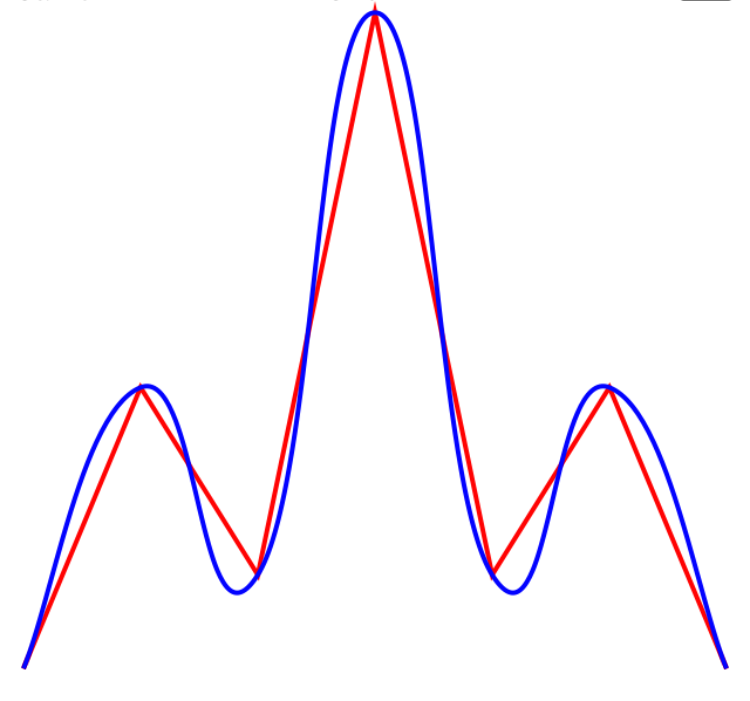
In the above figure, red line shows the points we have. blue line represents the cardinal curve we want to create. Cardinal curve goes through all the points.

UIBezierPath

First the basics. there are two kinds of curves in UIBezierPath. Both of the curves need additional control points to define the curvature. we will need to calculate the control points to generate a smooth curve passing through given points.

• Quadratic
• Cubic

Quadratic

Quadratic curve has one control point which defines how the curvature of the bezier should be.

[bezierPath addQuadCurveToPoint:destPoint controlPoint:cp1];

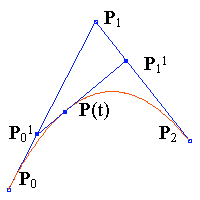
here P₀ is starting point and P₂ is ending point. P₁ is the Control Point.

Cubic

Cubic curve has two control ponints which define its curvature.

 [bezierPath addCurveToPoint:destPoint controlPoint1:cp1 controlPoint2:cp2];

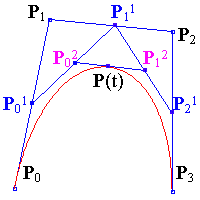
here P₀ is starting point and P₃ is ending point. P₁ is the Control Point 1.P₂ is the Control Point 2.

Cardinal Curves

This curve passes through all given points and each segment can be composed of cubic spline segments. We will need to figure out all the control points for each of the points.

Approximating with Cubic is easier and we go with that direction.

Solution

consider the control points we need. see that at T2, the handle is paralled to the neighboring points. in order to calculate this, we will compute the derivatives at each point which would give us the tangents.

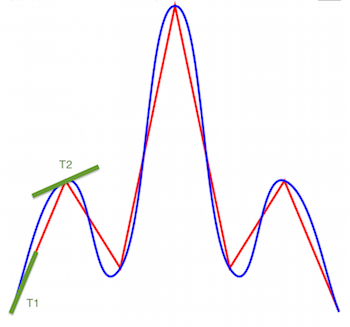
the green bars are the computed derivatives at each of the points. first and last points would go towards the neighboring points.

• each pair of points act as start and end of the curve
• for each start and end of curve we will compute the control points required
• for first and last point of the curve the control points will go towards the second and previous point respectively
• for any given point, the control points(T2) are tangents , tangent is parallel to previous two points and hence we can compute using derivatives at each point

Equations

Let P₀ , P₁ ... P_n be the points.

point derivatives can be computed by

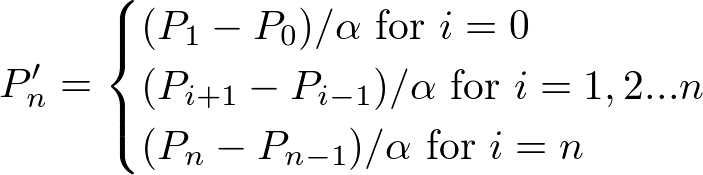
we need to calculate the control points from these. we can calculate those using.

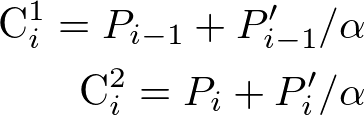
Once we have the control points, we can easily compose the Bezier Path.

Alpha is a tension. which gives the amount of smoothness needed in the curve.

ObjC Pseudo Code

    NSMutableArray *points = [[NSMutableArray alloc] init];
    //populate points with CGPoint

    NSMutableArray *derivative = [[NSMutableArray alloc] init];

    for(NSInteger j=0;j<points.count;j++) {
        CGPoint prev = points[MAX(j-1,0)];
        CGPoint next = points[MIN(j+1,points.count-1)];

        derivative[j] = (next - prev) / 2;
    }

    UIBezierPath *path = [UIBezierPath bezierPath];
    for(NSUInteger i=0;i<points.count;i++) {
        if(i==0) {
            [path moveToPoint:points[i]]
        } else {
            CGPoint endPoint = points[i];
            CGPoint cp1 = points[i-1]+ derivative[i-1]/tension;
            CGPoint cp2 = points[i] + derivatives[i]/tension;

            [path addCurveToPoint:endPoint controlPoint1:cp1 controlPoint2:cp2];
        }
    }

    return path;

Code

Complete project at : YKBezierAdditions